
1. Por qué sigo recurriendo a Magnus-Tetens cuando necesito el punto de rocío
Hace más de un siglo que las primeras estaciones meteorológicas automáticas empezaron a usar la fórmula de Magnus-Tetens para convertir temperatura y humedad relativa en un valor de punto de rocío casi instantáneo. Hoy ese mismo cálculo corre silencioso dentro de sensores domésticos, controladores de HVAC, servidores de previsión numérica e incluso en mis automatizaciones de Home Assistant: si el punto de rocío interior supera los 17 °C, mi extractor del baño se activa antes de que aparezca la primera gota de vaho.
Ese equilibrio entre simplicidad algebraica (una ecuación cerrada con dos o tres constantes) y precisión más que decente (±0,3 °C en la práctica) explica su vigencia frente a alternativas más complejas como Goff-Gratch o Hyland-Wexler. En este artículo voy a desmenuzar la historia, los fundamentos físicos y las variantes modernas de la ecuación; compararé su rendimiento con otros métodos y, sobre todo, te mostraré cómo ponerla a trabajar en Excel, Python o un microcontrolador ESP32 sin despeinarte.
2. De August a Tetens: una historia de refinamientos (y de poner apellido al hallazgo ajeno) 🔍
Cuando en 1844 el físico berlinés Heinrich G. Magnus encajó los datos de presión de vapor con su famosa curva exponencial, no imaginaba que un siglo después acabaría compartiendo portada con Otto Tetens. De hecho, si rascamos en los archivos descubrimos que el germen real venía de E. F. August (1828) y del francés P. Roche: ambos habían bosquejado fórmulas parecidas décadas antes. Magnus reconoció aquellas influencias, afinó los coeficientes y la comunidad meteorológica adoptó la ecuación con su apellido.
Tetens entró en escena en 1930 desde el Observatorio de Lindenberg. Aplicó la misma estructura exponencial pero recalibró los parámetros para climas templados, logrando errores de apenas 1 Pa entre −5 °C y 35 °C. Esa combinación de exactitud con “código fuente” corto catapultó la ecuación a los manuales de psicrometría… y a nuestros IDE actuales.
Resumen cronológico
• August & Roche (1828-1838) – primer molde matemático.
• Magnus (1844) – popularización y validación empírica.
• Tetens (1930) – reajuste de constantes y difusión masiva.
• Bolton, Sonntag, Buck (1960-1990) – micro-ajustes para rangos extremos.
Mirar atrás sirve para entender por qué circulan tantos juegos de constantes. No es dispersión, es evolución: cada autor pulió la ecuación para su problema concreto (climatología tropical, glaciología, calibración de sensores…), de ahí que hoy convivan pares tan famosos como 17,27 / 237,3 y 17,625 / 243,04.
3. Fundamentos físicos: cuando la esponja-aire se empapa
Piensa en el aire como en una esponja que puede retener vapor de agua. A mayor temperatura, la esponja se “hincha”: su presión de vapor de saturación Ps(T) crece de forma exponencial (ley de Clausius-Clapeyron). Si enfriamos la mezcla isobáricamente, esa capacidad baja hasta que, a la temperatura T<sub>dp</sub> (dew point), la esponja se satura y el exceso gotea.
La ecuación de Magnus-Tetens es, sencillamente, una aproximación empírica a Ps(T):
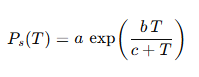
donde a, b y c se eligen para clavar la curva en el rango de interés. Con Ps en la mano, la humedad relativa se define como RH = 100 Pa ⁄ Ps(T). Bajar la incógnita y resolver T<sub>dp</sub> implica una única operación logarítmica adicional, lo que a principios del siglo XX era sinónimo de cálculo a mano apto para cualquier observador meteorológico armado con tablas.
4. La ecuación paso a paso (aire / hielo) y sus constantes estrella
4.1 Forma práctica moderna
Casi todas las calculadoras web —Omni incluida— usan la versión de Alduchov & Eskridge (1996):
γ(T,RH) = ln(RH/100) + (17.625·T)/(243.04+T)
Td = 243.04·γ / (17.625 − γ)
Con eso mantienes el error en ±0,35 °C entre −40 °C y 50 °C. Si solo trabajas sobre agua líquida (T>0 °C) y te basta con ±0,4 °C, el clásico 17,27 / 237,3 te resultará más fácil de memorizar.
4.2 Variantes que merece la pena conocer
| Finalidad | a | b (°C) | Extra | Precisión típica |
|---|---|---|---|---|
| Tetens (1930, agua) | 17.27 | 237.3 | c = 0.61078 kPa | ±0.3 °C (0-35 °C) |
| Tetens (hielo) | 21.875 | 265.5 | − | ±0.4 °C (−40-0 °C) |
| Bolton (1980) | 17.67 | 243.5 | − | ±0.1 % Ps (−30 – 35 °C) |
| Sonntag (1990) | 17.62 | 243.12 | − | ±0.35 °C (−45 – 60 °C) |
| Buck (1981, agua) | 18.678 | 257.14 | d = 234.5 | ±0.05 % Ps (0 – 50 °C) |
Regla de oro: cuanto más extremo sea tu rango (cámaras climáticas, procesado criogénico, desertificación), más te conviene migrar a Buck o incluso a Goff-Gratch. Para el 90 % de escenarios domésticos e industriales, Magnus-Tetens “estándar” sigue ganando la partida coste-beneficio.
4.3 Ejemplo exprés
Con T = 30 °C y RH = 60 %:
γ = ln(0.60) + (17.27·30)/(237.3+30) = 1.4242
Td = (237.3·1.4242) / (17.27−1.4242) ≃ 21.3 °C
Si la temperatura ambiente baja de 21 °C, verás condensación.
5. Cómo lo calculo a diario: de la libreta a Python y al YAML de Home Assistant
5.1 Hoja de cálculo
En Excel/LibreOffice basta con:
= (243.04*LN(B2/100)+(17.625*A2)/(243.04+A2)) /
(17.625-LN(B2/100)-(17.625*A2)/(243.04+A2))
donde A2 = temperatura y B2 = RH. Inserta un formato condicional para pintar en rojo cualquier Td por encima de 18 °C si quieres evitar moho.
5.2 Python minimalista
import math
def dew_point(t, rh):
γ = math.log(rh/100) + (17.625*t)/(243.04 + t)
return (243.04 * γ) / (17.625 - γ)
La función corre en un ESP32 bajo MicroPython sin problemas y redondea el resultado a dos décimas en 2 ms.
5.3 Automatización domótica
En Home Assistant puedes crear un sensor templado:
- platform: template
sensors:
dew_point_indoor:
friendly_name: "Punto de rocío interior"
unit_of_measurement: "°C"
value_template: >
{% set t = states('sensor.temp')|float %}
{% set rh = states('sensor.humidity')|float %}
{% set gamma = (0.66077*math.log(rh/100)) + ((17.27*t)/(237.3+t)) %}
{{ (237.3*gamma) / (17.27-gamma) | round(1) }}
En mi configuración, disparo un extractor si dew_point_indoor supera la temperatura de una tubería fría —me ahorró un episodio de condensación brutal el invierno pasado.
6. Aplicaciones reales: de la previsión de niebla al secado de aire comprimido
- Meteorología operacional
• El punto de rocío es mejor indicador de humedad específica que la RH. Cuando veo predicciones con Td cercano a la temperatura mínima nocturna, sé que habrá niebla o rocío intenso al amanecer.
• Pilotos VFR combinan T y Td para estimar la altura de base de nubes (regla de los 400 ft por °C). - HVAC y construcción
• Determinar la temperatura de rocío interior permite elegir el espesor de aislamiento o decidir si necesito doble ventana.
• En museos se mantiene Td por debajo de 14 °C para evitar hongos en lienzos. - Procesos industriales
• Sistemas de aire comprimido especifican Td ≤ −40 °C ISO 8573-1 (clase 1) para evitar corrosión en circuitos neumáticos. Magnus-Tetens corre embebida en los transmisores de Suto Itec que certifican esa clase.
• En secaderos de jamón, ajustar Td controla la deshidratación superficial y la floración de mohos deseables. - Domótica y confort
• Un sensor de Td me avisa si abrir ventanas secará el ambiente o lo empeorará. Si fuera el Td exterior está 5 °C por debajo del interior, ventilar es buena idea; si no, activo el deshumidificador.
7. Precisión, límites y cuándo saltar a otra ecuación
La mayoría de errores proceden de tres supuestos:
- Presión estática ≃ 1013 hPa. A 3 000 m de altitud el sesgo ronda +0,5 °C. Ajusta a o añade corrección barométrica si trabajas en alta montaña.
- Calor latente constante. Aumenta el error a >50 °C. Buck solventa la deriva con su parámetro d.
- Histéresis del sensor de RH. Un higrómetro de polímero barato tiene ±2 %RH de incertidumbre; eso se traduce en ±0,5 °C de Td, mayor que el error intrínseco de la ecuación.
Para laboratorios metrológicos lo habitual es correr una iteración de Newton-Raphson sobre Goff-Gratch o Hyland-Wexler, pero fuera de ese nicho Magnus-Tetens sigue siendo la navaja suiza.
8. Errores típicos que me he encontrado (y cómo los solucioné)
Error nº 1 — Usar 17,27/237,3 a −20 °C.
En una cámara de frío industrial los operarios obtenían Td diferentes según la app. El coeficiente 17,27 subestima Ps sobre hielo: cambiamos a la pareja 21,875/265,5 y la lectura coincidió con el higrómetro de referencia.
Error nº 2 — Olvidar el logaritmo natural.
Algún tutorial anglosajón usa logaritmo base-10 pero mantiene las constantes de Magnus. El resultado se dispara varios grados. Verifica siempre que ln sea natural.
Error nº 3 — Redondear RH a enteros.
Sensores que reportan 57 % en lugar de 56,7 % introducen ±0,3 °C de ruido. Si el control es crítico (por ejemplo en incubadoras), conserva al menos una décima.
9. Preguntas frecuentes
¿La fórmula sirve bajo presión no atmosférica?
Puedes corregir Ps multiplicando por la presión absoluta/1013 hPa; el error residual queda por debajo del 1 %.
¿Magnus-Tetens funciona con gases diferentes del aire?
Solo si su fracción de vapor de agua es dominante y la mezcla se comporta ideal; para CO₂ supercrítico, usa tablas específicas.
¿Existe una versión en grados Fahrenheit?
Sí, basta con convertir T y los coeficientes: b pasa a 432,85 °F en la pareja 17,625/243,04.
10. Conclusiones — Lo que deberías recordar antes de tu próximo cálculo
- La fórmula de Magnus-Tetens condensó un siglo de mediciones y sigue siendo la opción preferida cuando necesitas rapidez con un error < ±0,4 °C.
- Elige el par de constantes en función del rango térmico: Tetens para climas templados, Buck para precisión máxima, Bolton para estaciones meteorológicas estándar.
- Implementarla es trivial en hojas de cálculo, Python o YAML, y abre la puerta a automatizaciones valiosas: desde evitar moho en casa hasta cumplir ISO 8573-1 en aire comprimido.
- Conocer sus límites (presión, rangos extremos, histéresis de sensores) te permite saltar a ecuaciones más potentes solo cuando de verdad lo necesitas.
Sígueme a Youtube

